Mean, median, and mode are essential concepts in statistics that help us understand the central tendency of a dataset. These measures provide insights into the average value, middle value, and most frequent value of a given set of numbers. Whether you're a student, researcher, or professional, understanding these concepts is crucial for analyzing and interpreting data accurately. This article aims to provide a comprehensive overview of mean, median, and mode, along with their connections and applications.
In today's data-driven world, statistical analysis plays a vital role in decision-making. From businesses to academics, people rely on statistics to make informed choices. Central tendency measures like mean, median, and mode are the building blocks of statistical analysis. By understanding these concepts, you can gain deeper insights into datasets and make more accurate predictions.
This article will explore the definitions, formulas, and practical applications of mean, median, and mode. Additionally, we'll discuss the connections between these measures and how they interact with each other in various scenarios. By the end of this article, you'll have a solid understanding of how to use these measures effectively in your data analysis efforts.
Read also:Wayans Family Names The Iconic Dynasty In Comedy
Table of Contents
- Introduction to Mean Median Mode
- Definition and Calculation of Mean
- Definition and Calculation of Median
- Definition and Calculation of Mode
- Connections Between Mean Median Mode
- Applications of Mean Median Mode
- Key Differences Between Mean Median Mode
- Advantages and Limitations of Each Measure
- Practical Examples of Mean Median Mode
- Statistical Insights and Data Analysis
- Conclusion and Call to Action
Introduction to Mean Median Mode
Central tendency is a fundamental concept in statistics that helps us summarize and describe data. Among the most commonly used measures of central tendency are mean, median, and mode. These measures provide different perspectives on the "center" of a dataset. Understanding the connections between mean, median, and mode can help you interpret data more effectively and make informed decisions.
Mean represents the arithmetic average of a dataset, median is the middle value when data is arranged in ascending or descending order, and mode is the most frequently occurring value. Each of these measures has its own strengths and limitations, making them suitable for different types of data and scenarios.
In this section, we'll explore the basic definitions of mean, median, and mode, along with their importance in statistical analysis. By understanding these concepts, you'll be better equipped to analyze data and draw meaningful conclusions.
Definition and Calculation of Mean
What is Mean?
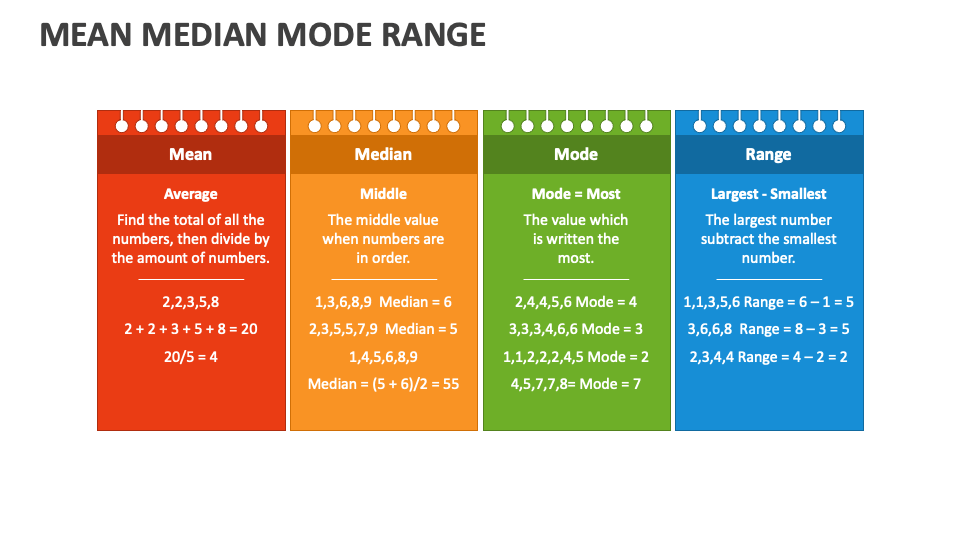
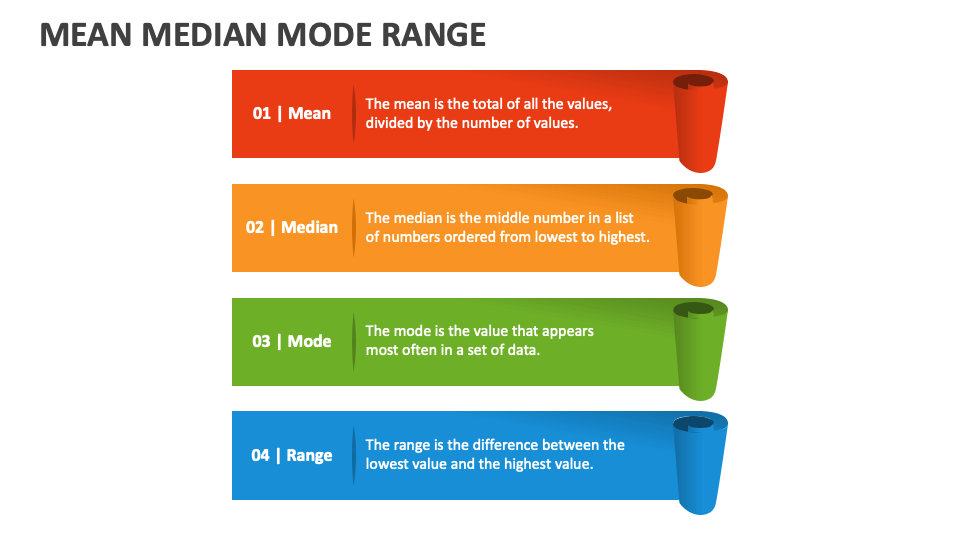
Mean, also known as the arithmetic average, is the sum of all values in a dataset divided by the number of values. It provides a single number that represents the "average" value of the dataset. The formula for calculating the mean is:
Mean = (Sum of all values) / (Number of values)
For example, if you have a dataset of 5 numbers: 10, 20, 30, 40, and 50, the mean would be:
Read also:Randy Ortons Son Exploring The Life And Legacy Of A Wrestling Dynasty
(10 + 20 + 30 + 40 + 50) / 5 = 30
Applications of Mean
Mean is widely used in various fields, including finance, education, and healthcare. It is particularly useful when dealing with datasets that are normally distributed and do not contain extreme outliers. However, mean can be skewed by outliers, making it less reliable in certain situations.
According to a study by the National Center for Education Statistics, mean scores are often used to evaluate student performance and compare educational outcomes across different regions.
Definition and Calculation of Median
What is Median?
Median is the middle value in a dataset when the values are arranged in ascending or descending order. If the dataset has an odd number of values, the median is the middle value. If the dataset has an even number of values, the median is the average of the two middle values.
For example, consider the dataset: 5, 10, 15, 20, 25. The median is 15 because it is the middle value. In the dataset: 5, 10, 15, 20, the median is (10 + 15) / 2 = 12.5.
Advantages of Median
Median is less affected by outliers compared to mean, making it a more robust measure of central tendency in skewed datasets. It is particularly useful in fields such as economics and social sciences, where datasets often contain extreme values.
A study by the World Bank highlights the importance of median income as a measure of economic well-being, as it provides a more accurate representation of the typical income level in a population.
Definition and Calculation of Mode
What is Mode?
Mode is the value that appears most frequently in a dataset. A dataset can have one mode (unimodal), two modes (bimodal), or multiple modes (multimodal). If no value appears more than once, the dataset has no mode.
For example, in the dataset: 3, 5, 5, 7, 9, the mode is 5 because it appears twice. In the dataset: 2, 4, 6, 8, there is no mode because all values appear only once.
Applications of Mode
Mode is particularly useful in categorical data analysis, where numerical calculations are not applicable. It is commonly used in market research, customer surveys, and opinion polls to identify the most popular choice or preference.
According to a report by the Pew Research Center, mode is often used to analyze survey responses and identify trends in public opinion.
Connections Between Mean Median Mode
The relationships between mean, median, and mode depend on the distribution of the dataset. In a perfectly symmetrical distribution, such as a normal distribution, the mean, median, and mode are equal. However, in skewed distributions, these measures can differ significantly.
In a positively skewed distribution, the mean is greater than the median, which is greater than the mode. In a negatively skewed distribution, the opposite is true: the mean is less than the median, which is less than the mode.
Understanding these connections can help you choose the most appropriate measure of central tendency for your analysis. For example, if your dataset contains extreme outliers, median may be a better choice than mean.
Applications of Mean Median Mode
Real-World Examples
Mean, median, and mode have numerous applications across various fields. In finance, mean is used to calculate average returns on investments, while median is used to analyze income levels in a population. In healthcare, mode is used to identify the most common symptoms or diagnoses in a patient population.
For instance, a study published in the Journal of Epidemiology found that median age was a more reliable indicator of disease prevalence in a population compared to mean age, especially in populations with significant age disparities.
Practical Uses in Business
In business, mean is often used to calculate average sales or profits, while median is used to analyze employee salaries or customer satisfaction scores. Mode is used to identify the most popular products or services, helping businesses make data-driven decisions.
Key Differences Between Mean Median Mode
- Mean: Arithmetic average of a dataset; sensitive to outliers.
- Median: Middle value of a dataset; less affected by outliers.
- Mode: Most frequent value in a dataset; useful for categorical data.
Each measure has its own strengths and limitations, making them suitable for different types of data and scenarios. Choosing the right measure depends on the nature of the dataset and the specific analysis requirements.
Advantages and Limitations of Each Measure
Advantages
- Mean: Provides a single value that represents the entire dataset; widely used in statistical analysis.
- Median: Less affected by outliers; useful in skewed distributions.
- Mode: Easy to calculate; useful for categorical data.
Limitations
- Mean: Can be skewed by outliers; not suitable for categorical data.
- Median: May not represent the entire dataset; less informative in symmetric distributions.
- Mode: May not exist in some datasets; less informative in numerical data.
Understanding the advantages and limitations of each measure can help you choose the most appropriate tool for your analysis.
Practical Examples of Mean Median Mode
Let's consider a real-world example to illustrate the use of mean, median, and mode. Suppose you are analyzing the test scores of a class of 20 students. The scores are as follows:
50, 60, 60, 70, 70, 70, 75, 80, 80, 80, 80, 85, 90, 90, 90, 95, 100, 100, 100, 100
- Mean: (50 + 60 + 60 + 70 + 70 + 70 + 75 + 80 + 80 + 80 + 80 + 85 + 90 + 90 + 90 + 95 + 100 + 100 + 100 + 100) / 20 = 81.5
- Median: (80 + 80) / 2 = 80
- Mode: 80 (appears 4 times)
This example demonstrates how mean, median, and mode can provide different perspectives on the same dataset.
Statistical Insights and Data Analysis
Statistical analysis often involves combining mean, median, and mode to gain a comprehensive understanding of a dataset. By analyzing these measures together, you can identify patterns, trends, and anomalies in your data.
For example, a study by the Centers for Disease Control and Prevention (CDC) used mean, median, and mode to analyze health data and identify risk factors for chronic diseases. This approach helped researchers develop targeted interventions to improve public health outcomes.
Conclusion and Call to Action
In conclusion, mean, median, and mode are essential tools for analyzing and interpreting data. Each measure provides unique insights into the central tendency of a dataset, making them valuable for a wide range of applications. By understanding the connections and differences between these measures, you can choose the most appropriate tool for your analysis and make more informed decisions.
We encourage you to apply these concepts in your own data analysis efforts and share your experiences with us. Leave a comment below or explore other articles on our website for more insights into statistics and data analysis. Together, we can unlock the power of data and drive meaningful change in our world.